Jak vzniká věc z 3D tiskárny? Že se vůbec ptám. Připravit STL model, pak pomocí sliceru převést na G-code a hurá tisknout… V tomto článku ale učiníme ještě krok zpět, před tvorbu trojrozměrného modelu. Máme problém z reálného světa, který chceme vyřešit pomocí 3D tisku. A já vás provedu procesem, který lze při řešení tohoto problému využít. Tisk je tentokrát jenom třešničkou na dortu.

Budeme totiž vyrábět náhradní díl ke kancelářské židli. A k modelování tentokrát použijeme bezplatný software OpenSCAD. Ten může možná na nováčky působit nepřístupným dojmem, protože nevyužívá klasické vizuální modelování, ale namísto toho se v něm objekty programují. Má to ale své výhody. Vtip je v tom, že můžete objekty parametrizovat – vytvoříte si obecný předmět, například ozubené kolo a pouhou změnou proměnných můžete jednoduše měnit jeho velikost, počet zubů a další parametry. Že to není až tak složité, si ukážeme na praktickém příkladu v následujících kapitolách.

Definice problému

Většina levných kancelářských židlí vypadá zespodu nějak takto:

Plastový knoflík, kterým se nastavuje vzdálenost opěradla od sedáku, ovšem vzal na jedné z našich židlí za své a zbyl jenom holý šroub:

O estetiku nám v tomto případě vážně nejde, protože spodní část židle stejně není vidět. Ale prostý šroub je příliš úzký, opěradlo tím pádem moc nedrží a viklá se. Což mne popouzí již drahnou dobu, a tudíž jsem před několika lety slíbil, že s tím něco udělám. A podle hesla „když chlap slíbí, že něco udělá, tak to taky udělá a netřeba mu to každý půlrok připomínat” na to přišla řada právě dnes.

Návrh řešení

Potřebujeme vyrobit náhradní knoflík, který opěradlo udrží na místě. Nemáme nejmenší tušení, jak vypadala původní součástka a jaká byla její konstrukce. Nebudeme tedy vyrábět přesnou kopii, ale díl, který bude funkčně ekvivalentní. Chceme součástku, která udrží opěradlo na místě a bude dostatečně odolná a snadno vyrobitelná na 3D tiskárně.

Potřebný díl je v principu velmi jednoduchý. V průřezu bude součástka vypadat přibližně takto:

Modrý obrys bude v podstatě válec s dírou, do které se schová šroub. Jeho přitažením pak budeme regulovat sílu, kterou bude opěradlo drženo na místě. Díl bude namáhán kompresí, což je parametr, který 3D tištěné díly zvládají velmi dobře. Namáhaná oblast bude zejména pod hlavičkou šroubu a mezi dílem a kovovou částí židle.

Mezi židli a díl můžeme vložit kovovou podložku, která tomu částečně pomůže, zejména bude-li široká. Pod hlavičku šroubu ovšem nic moc dát nemůžeme, protože otvor pro ni musí být šestihranný a těsný, aby šroubem bylo možné otáčet. Nicméně průzkum kancelářských židlí v okolí přinesl zjištění, že tyto díly bývají běžně plastové, takže to namáhání nebude nikterak kritické.

Měření

Konstrukce náhradního dílu zpravidla začíná měřením. Uchopíme tedy šupleru a změříme několik parametrů, viz obrázek níže.

Reálně potřebujeme znát vzdálenost označenou na obrázku jako a1 – vzdálenost mezi sedákem židle a spodní částí hlavy šroubu. A potřebujeme ji znát jako minimální vzdálenost (když je šroub plně zašroubovaný a kouká jenom nejkratší část) a maximální vzdálenost (když je šroub skoro vyšroubovaný a drží jen na posledních pár závitech). Síla našeho dílu musí být někde mezi těmito hodnotami. Pokud by byl příliš tenký, bude volně plandat a nebude plnit svou funkci. Pokud by byl příliš silný, nepůjde šroub zašroubovat a díl bude rovněž k ničemu.

Přímé změření požadovaného rozměru není v tomto případě úplně triviální, protože nám překáží sedák a konstrukce židle. Změříme tedy rozměr a3 (to je snadné) a odečteme od něj tloušťku hlavy šroubu (a2).

Dále pak potřebujeme znát průměr šroubu a průměr kružnice opsané hlavě šroubu. Tedy rozměr označený d_o, nikoliv d_i. Proč zrovna kružnici opsanou? Bude se nám hodit později při vytváření modelu v OpenSCADu, kde lze se znalostí průměru kružnice opsané snadno vytvořit potřebný tvar.

Další součástí výbavy bude blok a tužka.

Z tohoto nákresu by nejspíš pan Smrt, můj učitel technického kreslení na průmyslovce, měl smrt, protože rozhodně neodpovídá normám pro technické výkresy. Nicméně pro operativní použití je dobrý dost. Vyčteme z něj podstatné rozměry, totiž:

• Jde o šroub M8, tedy o normovaném průměru 8 mm (že jsme naměřili 7,7 mm je dáno závitem, jeho opotřebováním a pouze přibližnou přesností plastové šuplery).
• Průměr opsané kružnice hlavy je 15 mm (na nákresu 14,7 mm).
• Tloušťka aktivní části dílu (okolo závitu) musí být nejméně 4 a nejvýše 17 mm. Uděláme ji 10 mm, takže bude dostatek manévrovacího prostoru.
• Tloušťka horní části dílu musí být nejméně 5 mm, aby se do ní vešla celá hlava šroubu. Větší tloušťka ničemu nevadí (naopak může pomoci snazší manipulaci), ale z mechanického hlediska ničemu nepomůže. Celkovou tloušťku dílu jsem stanovil na 30 mm, aby dobře padnul do ruky.
• Vnější průměr knoflíku stanovíme rovněž odhadem na 50 mm.

Poznámka k rozměrům: Parametry šroubů jsou normované a se znalostí průměru (M8) bychom mohli rozměry hlavy najít v normách. Každopádně pro účely naší amatérské konstrukce je snazší rozměry změřit než je hledat v tabulkách. Nicméně pokud hodláte konstruovat například raketoplán, je na místě exaktnější přístup 🙂

Modelování

Se znalostí potřebných rozměrů se můžeme vrhnout na modelování. Výběr nástroje je sice v konečném důsledku na vás, my v tomto případě volíme OpenSCAD, protože na podobné věci se hodí výborně a zaslouží si trochu zviditelnit.

Začneme tím, že si jako proměnné nadefinujeme výše uvedené rozměry a vytvoříme válec o celkových vnějších rozměrech a odečteme od něj díru pro šroub (zatím bez hlavy):

Výsledek v OpenSCADu vypadá takto:

Díra je ale potažena jakousi „membránou”, kterou v našem modelu nechceme. OpenScad tímto způsobem ukazuje stěnu o nulové šířce. Konce díry nahoře a dole mají nulovou šířku, protože jsme odčítali přesné rozměry.

Tento efekt odstraníme tím, že odečítaný válec díry uděláme o kousek větší a posuneme ho tak, aby větší válec trochu přesahoval. Výsledný kód bude vypadat následovně:

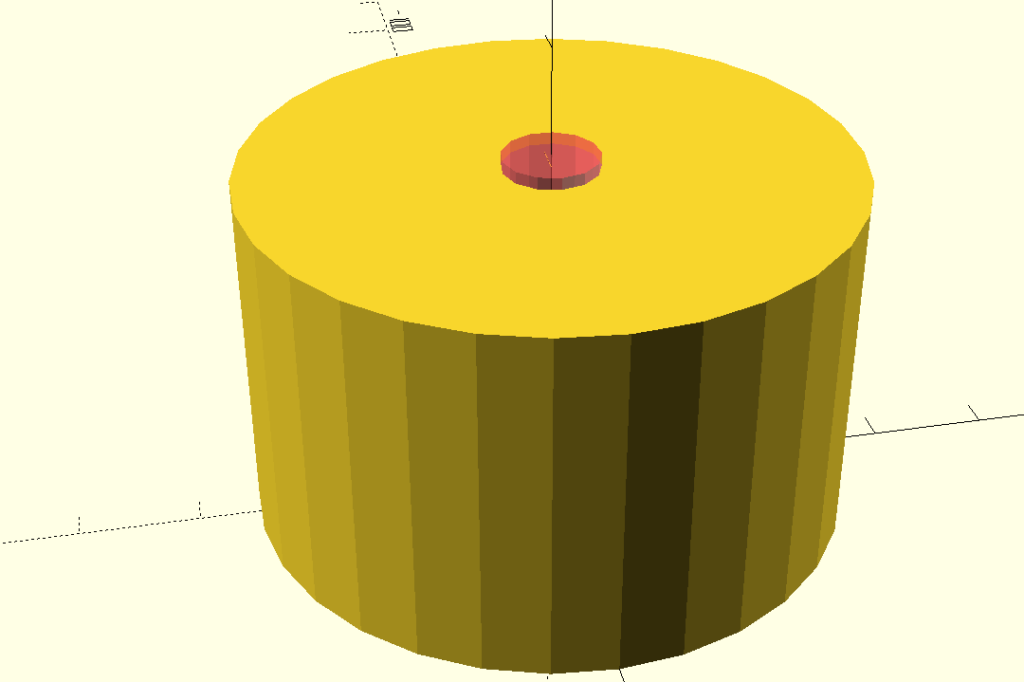
Model v OpenSCADu vypadá takto (přečnívající válec je pro názornost vidět a zobrazen červeně. Ve skutečnosti je v modelu prostě díra):

Jak je z obrázku vidět, OpenSCAD neumí udělat oblou plochu. Stěnu válce rozkouskuje na spoustu krátkých úseček – z kružnice tedy udělá mnohoúhelník. Počet dílů lze určit pomocí systémové proměnné $fn. Vyšší čísla budou mít za následek oblejší válec, ale také se tím zvýší složitost modelu a doba jeho renderování. Parametr $fn můžeme nastavit globálně, pro celý model, nebo jako argument metody cylinder. My jej globálně nastavíme na 64:

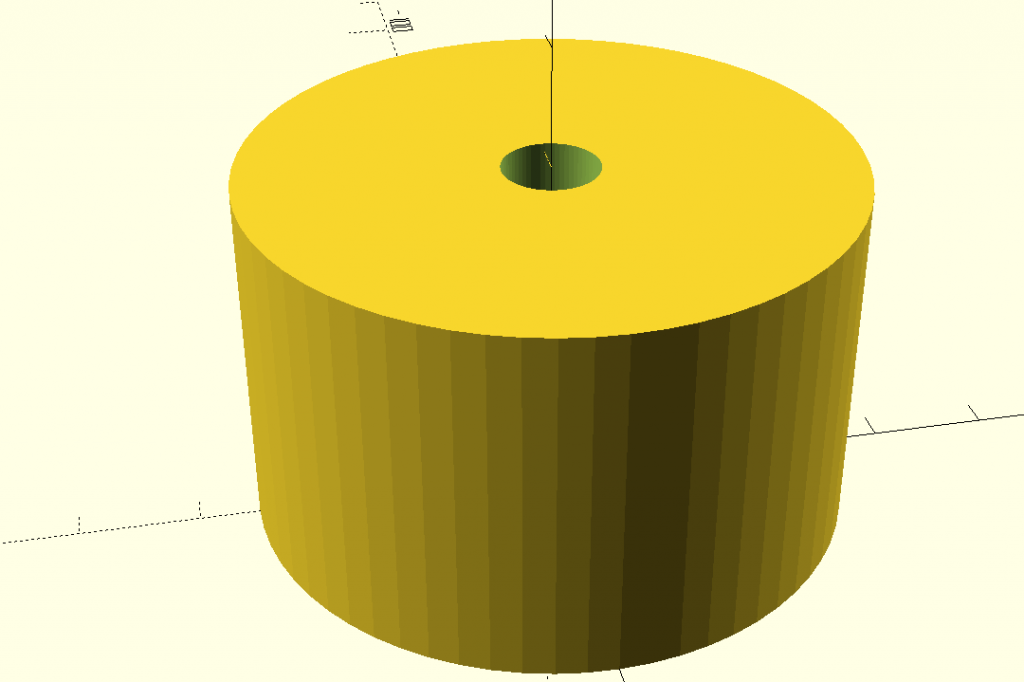
Válec je nyní o poznání kulatější:

Průměr válce je zadáván jako velikost kružnice opsané mnohoúhelníku, jehož počet stran je určen parametrem $fn. Proto jsme u hlavy šroubu měřili právě tento rozměr. Nastavením $fn = 6 snadno vytvoříme díru o půdorysu šestistěnu:

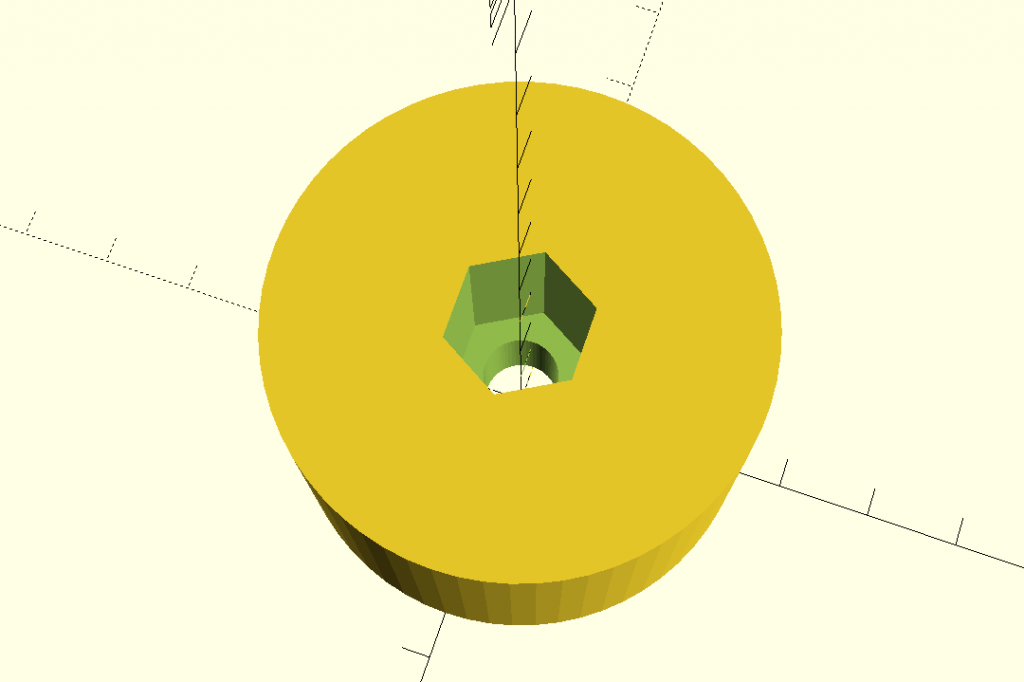
Výsledek už vypadá docela slibně:

U děr je tedy nutné mít na paměti, že vzhledem ke své konstrukci budou reálně menší, než jak byly nastaveny. O další zmenšení se pak postará přímo technologie FDM tisku, která má tendenci díry trochu „zalévat”.

Upravíme proto kód tak, že přidáme k oběma dírám toleranci +0,5 mm. Tuto hodnotu jsem určil empiricky jako osvědčenou na základě praxe:

Model je v podstatě hotový. Jenže hladký díl byste utahovali obtížně, proto uděláme stěnu vroubkovanou. Nejsnazší způsob, jak toho dosáhnout, je umístit po obvodu válce menší válečky, které do hlavního dílu zčásti zapustíme. Budou nám k tomu stačit v podstatě jen znalosti z druhého stupně základní školy. Začněme výpočtem požadovaného průměru válečku (knurl_diameter). Ten spočítáme tak, že obvod kruhu vydělíme počtem segmentů $fn. Z vlastní zkušenosti vím, že válečky vypadají lépe, pokud jsou trošku větší, tudíž vše ještě vynásobíme koeficientem 1.5:

Dále musíme spočítat umístění válečků (knurl_step). Jednoduše vydělíme 360° počtem segmentů $fn a opět na základě empirických zkušeností vynásobíme dvěma, aby k sobě válečky těsně nepřiléhaly.

Nyní se dostáváme k nejsložitější části kódu, protože pro umístění válců musíme použít cyklus for. Absolutní polohu válců (proměnné dx a dy) spočítáme pomocí goniometrických funkcí sinus a kosinus na základě znalosti poloměru válce a úhlu, kde postupně v kroku knurl_step projdeme celých 360° v cyklu for.

Jen rychlé vysvětlení: válečky vypadají lépe, pokud jsou do těla objektu zapuštěné (proto se odčítá -1, tedy 1 mm). Posun úhlu o třetinu kroku ( knurl_step / 3) je využit proto, aby válečky zakryly ostré hrany na těle objektu. Má sice 64 stěn, stále ovšem není zcela hladký, tudíž hrany takto chytře zamaskujeme. U malých válečků stačí pouze 16 stran ($fn = 16).

Výsledný kód vypadá následovně:

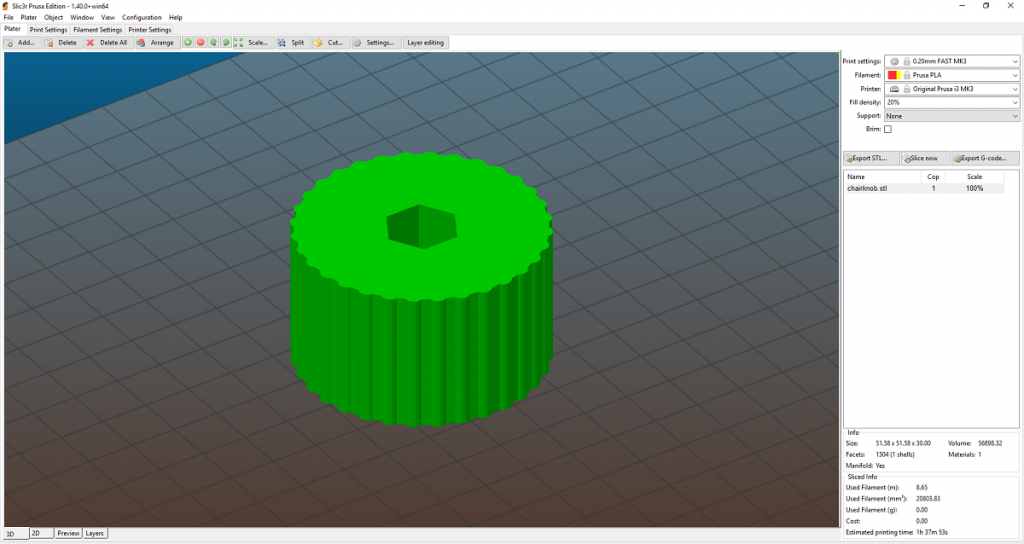
Konečná podoba modelu je funkční, a dokonce i vcelku estetická, přestože o vzhled nám primárně nešlo:

Tisk

Výsledný model vyrenderujeme a vyexportujeme z OpenSCADu v klasickém formátu STL. Model pak naimportujeme do Slic3r PR, kde proběhne i automatická detekce neuzavřených ploch a případná oprava geometrie. Model je navržen pro jednoduchý tisk, nejsou tedy potřeba žádné podpory ani jiné speciální postupy. Pro tisk vám postačí obyčejné PLA s 20% infillem. U této součástky nepředpokládáme, že bude nějak teplotně namáhána a z mechanického hlediska je PLA dostatečné. Tisknout samozřejmě můžete i z PETG nebo ABS, ničemu to neuškodí.

Nyní stačí necelých devět metrů filamentu a za zhruba hodinku a půl je výrobek hotový.

Sestavení a testování

Výsledný výtisk doplníme podložkou, aby se rozložila zátěž na místech, kde se přítlačné kolečko dotýká kovové konstrukce židle. Je vhodné použít nikoliv standardní M8 podložku, ale širší, na fotografii vpravo.

Nyní stačí vyšroubovat šroub, vložit jej do vytištěného dílu, dát pod něj podložku a zašroubovat. Funguje stejně dobře jako originál a vzhledem k robustnější konstrukci bude nejspíše i odolnější.

Slovo závěrem

V nejrůznějších návodech pro začátečníky či mírně pokročilé je většinou nejvíce prostoru věnováno klasickým modelovacím nástrojům jako je Fusion360, Blender, 3D Studio Max či řadě CADových programů. OpenScad sice může působit na první pohled složitě, ale v tomto článku jsme si na praktickém příkladu ukázali, že to zas až tak hrozné není. Schválně si zkuste hodnoty v kódu různě modifikovat, a sledujte, jak to ovlivní výsledný model. O OpenScadu rozhodně neslyšíte naposledy, příště se podíváme na něco o chlup složitějšího.

OpenScad můžete zdarma stáhnout z oficiálních stránek.

A můžete si stáhnout i vygenerovaný .stl model.